Wanneer we een vraag voorgeschoteld krijgen waarop we het antwoord niet weten dan gaan we automatisch gokken op de uitkomst en laten ons leiden door ons buikgevoel of intuïtie. Volgens het woordenboek is intuïtie: “direct weten zonder te redeneren”. Het probleem is dat intuïtie meestal totaal verkeerd uitdraait. Een paar voorbeelden:
Indien we een boek van 250 pagina’s willen lezen en we hebben het voornemen om elke dag 25 pagina’s te lezen dan weten we dat na 10 dagen het boek is uitgelezen. Maar hebben we meer of minder dagen nodig als we beslissen om de eerste dag 1 pagina te lezen en elke daaropvolgende dag telkens het dubbel aantal pagina’s te lezen. Dus dag 1, 1 pagina; dag 2, 2 pagina’s; dag 3, 4 pagina’s, dag 5, 8 pagina’s enzovoort (dus op dag 5 hebben we in totaal 15 pagina’s gelezen, merkelijk minder dan na 1 dag in de vorige aanpak waar we elke dag 25 pagina’s lezen). Wat is uw intuïtie? Het antwoord op het einde van deze bijdrage.
Jaren terug was er tijdens de zomer op TV een spelprogramma (ik denk gepresenteerd door Geert Hoste maar twijfel hierover). Drie kandidaten kregen een kwis voorgeschoteld met kennisvragen en/of een behendigheidsproef om de kandidaten te rangschikken. Er waren 3 strandcabines en in één van die cabines lag een prijs verborgen, de twee andere cabines waren leeg. De eerst gerangschikte mocht als eerste een strandcabine aanduiden. Indien de cabine leeg was, mocht de tweede gerangschikte kandidaat een cabine kiezen. Indien de prijs nog niet gevonden was mocht de laatste gerangschikte de overgebleven cabine aanduiden met de prijs. Elke dag opnieuw deden de kandidaten hun stinkende best om als eerste te mogen kiezen. Maar is dat wel de correcte strategie? Welke plaats geeft U het meeste kans om met de prijs naar huis te gaan? Het antwoord op het einde van deze bijdrage.
Een derde voorbeeld: Stel dat je als 50-jarige een te hoog cholesterolgehalte hebt. De dokter legt uit dat er 3 medicijnen beschikbaar zijn. Van het eerste medicijn moet je gedurende 5 jaar, elke dag een groen pilletje nemen zodat de kans op overlijden aan een hartinfarct (ten gevolge een te hoge cholesterolwaarde) met 33% afneemt ten opzichte van een controlegroep. Van het tweede medicijn, moet je ook gedurende 5 jaar, elke dag een rood pilletje nemen zodat de kans op overlijden aan hartfalen van 3 naar 2% verminderd. Er is ook nog een derde medicijn, waarvan je weerom gedurende 5 jaar, elke dag een wit pilletje moet nemen en dan zal de kans op sterfte door hartfalen met 1% verminderen. Voor welk medicijn kies je? Waarschijnlijk kies je voor de groene pilletjes omdat die het sterftecijfer met 33%, het hoogste percentage verminderen. Maar eigenlijk zou je naar de prijs per pilletje moeten vragen en kiezen voor het goedkoopste medicijn. Behalve de kleur en eventueel de prijs, verschillen deze drie medicijnen niet van elkaar in het verhinderen van hartfalen bij patiënten. Van de 100 personen van 50 jaar, zullen er statistisch gezien 3 personen (= 3% van de bevolking) na 5 jaar overlijden aan een hartinfarct ten gevolge een te hoog cholesterolgehalte. Wanneer je getrouw de pilletjes neemt dan zakt het aantal personen die sterven van 3 naar 2 personen (=33%) op honderd mensen, slechts 1 minder dode per honderd personen (1%). In dit geval ben je niet misleid door de dooddoener “met statistiek kun je alles bewijzen” maar je hebt intuïtief een beslissing genomen zonder rekening te houden met beschikbare gegevens.
De voorbije weken was ik als vrijwilliger actief in het vaccinatie centrum ‘Markthalle Overijse’. Daar bleek dat vele mensen schrik hebben om Vaxzevria, het AstraZeneca vaccin toegediend te krijgen. Het lijkt zelfs op een angstpsychose door de geruchten en nieuwsberichten die ze gehoord of gelezen hebben. Nochtans Boris Johnson verkondigt dat zijn AstraZenica vaccin uiterst betrouwbaar en nuttig is. Als ik het goed voor heb weigert Denemarken en Noorwegen het Vaczevria nog te gebruiken en in België heeft men beslist om geen AstraZenica vaccin meer toe te dienen aan personen jonger dan 41 jaar. Een paar dagen geleden werd aangekondigd dat er twee Belgen (hun leeftijd werd niet medegedeeld) overleden waren ten gevolge trombose-gerelateerde complicaties. Hoe zit dat nu? Al die regeringen laten zich toch bijstaan door experten virologen, biostatistica, epidemiologen, dokters, etc… . Waarom zijn er dan verschillende maatregelen in verschillende landen? En als wij Vaxzevria niet meer of veel minder gaan gebruiken, is het dan verdedigbaar om dat vaccin aan Afrikaanse landen te doneren? Laat ons de intuïtie of buikgevoel even achterwegen laten en de gegevens analyseren. We kunnen ervan uitgaan dat alle vaccins evengoed de verschillende varianten neutraliseren, ook zijn de verschillende varianten in zowat elk westers land evenwaardig verspreid. Het grote verschil ligt in de verschillen in infectiegolf en voor een stuk in de verschillen in de leeftijdspiramide die er in deze landen heerst.
Een recent artikel in het vaktijdschrift Science geeft duidelijkheid. Ten eerste, er bestaat niet de minste twijfel over het groot voordeel van het vaccin voor de ganse populatie van een land of regio om de dodelijke afloop na een Covid19 te ontlopen of drastisch te verminderen ten opzichte van de minieme risico’s op mogelijke bloedproblemen. Deze verontrustende bloed complicaties komen voornamelijk – maar niet uitsluitend – voor bij vrouwen onder de 60 jaar. (In het Verenigd Koninkrijk waren onder de 209 gevaccineerden met trombose, 87 mannen en 120 vrouwen en in 139 van de gevallen waren de patiënten jonger dan 60 jaar). In Duitsland, Denemarken circuleren soortgelijke getallen.
Tabel 1: Vermeden hospitalisaties en vermeden doden door Vaxzevria vaccinatie per 100.000 inwoners in een regio met veel infecties (rode cijfers) of in een regio met weinig infecties (blauwe cijfers) en dit voor de verschillende leeftijdsgroepen. Het aantal personen met bloed complicaties per 100.000 gevaccineerden (zwarte cijfers in kolom in het midden) is onafhankelijk van het aantal besmettingen in de regio.
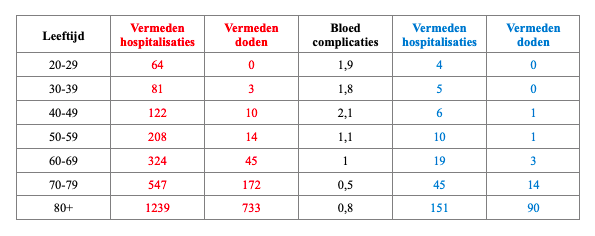
In de verdere analyse onderzoeken we de grootte van het risico van naderbij en wie het meest kwetsbaar is. Na de vaccinaties met Vaxzevria hebben 8,75 mensen op 100.000 bloedstollingsproblemen vertoond (belangrijk: niet alle bloedstollingsproblemen hebben een dodelijke afloop). Niet alle leeftijdsgroepen hadden dezelfde graad van problemen. Zo kwamen de problemen bvb tweemaal meer voor bij de groep tussen 20-29, 30-39,en 40-49 jaar (telkens ca 2 per 100.000) dan bij 50-59 en 60-69 jaar (ca 1/100.000), en nog minder bij de 70-79 jarigen (0,5/100.000) en 80+ (0,8/100.000) (zie tabel kolom in het midden).
Deze cijfers zijn onafhankelijk of er gevaccineerd werd in gebieden waar veel infecties woeden of in gebieden met weinig infecties. De sleutelvraag is echter: “hoeveel hospitalisaties werden vermeden door te vaccineren en hoeveel doden werden er minder geteld bij de gevaccineerden?” Het totaal aantal gehospitaliseerde Covid19 patiënten is afhankelijk van het aantal infecties. Daarom geven we in de tabel de cijfers van het aantal vermeden hospitalisaties en vermeden doden over een periode van 4 maand in een regio waar 886 infecties per 100.000 inwoners per maand genoteerd werden ( (Linker kolommen in de tabel) en in een regio waar er slechts 55 corona infecties bevestigd werden (per maand en per 100.000 inwoners) (rechter kolommen in de tabel).
De vermeden gehospitaliseerden en doden worden per leeftijdsgroep van 10 jaar weergegeven. Wat opvalt is dat voor de min 40-jarigen (= 20-39 jaar) in gebieden met lage infectie 0 doden voorkomen na gevaccineerd te zijn terwijl er toch voor deze groep ca 4 personen onder de 100.000 met bloedstollingsproblemen te verwachten vallen, waarvan een fractie kan overlijden. Voor de 60+ zien we dat gemiddeld 2,3 gevaccineeerden bloed complicaties zullen vertonen. Dit is een peulschil ten opzichte van de 107 Covid19 doden die vermeden werden, zelfs bij lage incidentie van infectie. Dus bij lage graad van infectie zullen we bij de ‘jongeren’ onder de 40 jaar niemand van de dood redden door te vaccineren, terwijl er toch een 4-tal op 100.000 problemen kunnen krijgen ten gevolgde Vaxzevria. Zelfs bij hoge infectiegraad brengt een vaccinatie niet veel verbetering tegenover de bloedstollingsproblemen voor de mensen onder de 40 jaar.
In het licht van die cijfers is de beslissing van onze regering om geen AstraZenica vaccin toe te dienen bij mensen onder de 41 jaar de enige juiste beslissing. Johnson heeft voor zijn beurt gesproken op een moment dat voornamelijk de oudere bevolking met Vaxzevria gevaccineerd werd. Als we de lijn doortrekken dan zou het ook geen goede beslissing zijn om Vaxzevria door te schuiven naar Afrikaanse landen. Die zitten doorgaans met een jongere bevolking (veel minder 60+ dan in west Europa) en de Covid19 infecties blijven voorlopig vrij laag. Het vrijgeven van Pfizer of Moderna vaccins zou uiteraard wel kunnen.
Omdat we verwachten dat in de toekomst, de infectiegraad in de EU sterk zal afnemen kunnen we de beslissing van EU om geen extra AstraZenica vaccins aan te schaffen ook begrijpen en toejuichen.
Oplossingen van eerder gestelde vragen:
- Een boek van 250 pagina’s is uitgelezen na 8 dagen indien men elke dag het dubbel aantal pagina’s leest tov de dag ervoor. Dat wordt: 1+2+4+8+16+32+64+128 = 255 pagina’s. Je zal de achtste dag wel de helft van het boek moeten lezen. Dus we hebben twee dagen minder nodig dan voor de strategie waarin men elke dag 25 pagina’s leest.
- Voor onze strandcabine kwis: alhoewel iedereen liefst als eerste aan de beurt komt om te kiezen, maakt het allemaal niks uit. De eerste kandidaat moet uit 3 strandcabines kiezen en slechts 1 cabine bevat een prijs. De kans om juist te gokken is dus 1/3. De tweede kandidaat heeft slechts 2/3 kans dat zij/.hij aan bod komt om te kiezen, maar zij/hij zal wel 1 kans op 2 hebben om juist te gokken. Dus de uiteindelijke kans is 2/3 x 1/2 = 1/3. De laatste kandidaat heeft slechts 1 kans op 3 dat hij/zij aan bod komt, maar als hij/zij aan bod komt is men zeker dat de prijs zich in die strandcabine bevindt.
[Een bijdrage van Serge Muyldermans]













